Closed Form Solution


What is Closed Form Solution?

Let’s say we are solving a Linear Regression problem. The basic goal here is to find the most suitable weights (i.e., best relation between the dependent and the independent variables). Now, there are typically two ways to find the weights, using

  1. Closed Form Solution
  2. Gradient Descent

A Closed-Form Solution is an equation which can be solved in terms of functions and mathematical operations and Gradient Descent is more of an iterative approach.

In order to get the weight(s) vector - θ we take the derivative of the cost function and do some geeky calculations (which you will learn in class) to arrive at the following equation:

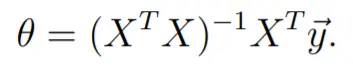Figure 1. Closed Form Solution

Here:

X - data (dependent variables)
y - target (independent variable)

In simpler terms, we multiply the data with its transpose, take the inverse of that matrix, multiply that again by the transpose and the target variable.

What do we achieve by doing so?

Liner Regression, yes, this is all there is to linear regression if approached via closed-form solution method.

But, Machine Learning wouldn’t be this much fun if things were so straight forward, right?

Figure 2. Constraints of Close-Form Solution for Linear Regression

As expected, there are some constraints which we need to keep in mind while using Closed-Form Solution and they are:

  1. The data should be a full rank matrix. The solution will not exist if data is not full ranked.
  2. For a matrix of size (n,m), n>=m, i.e. # of rows should be greater than or equal to # of columns.

Limitations and Advantages

Major drawback of this method is that, typically, we cannot use Closed-Form Solution on very large datasets. This is because, we cannot invert large datasets,

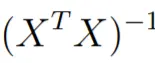Figure 3. Matrix Inversion

part of the equation. Why can we not invert? Because the computer will run out of memory while trying to do so.


The advantage is that, this method is really quick compared to Gradient Descent. Hence proving to be time efficient.