Linear Regression

Figure 1. Lets Begin
1. What is Linear Regression?
Linear regression is a basic and commonly used type of predictive analysis. The overall idea of regression is to examine two things:
- Does a set of predictor variables do a good job in predicting an outcome (dependent) variable?
- Which variables in particular are significant predictors of the outcome variable, and in what way do they–indicated by the magnitude and sign of the beta estimates–impact the outcome variable.

Figure 2. Confusion
In simpler terms….
Linear Regression is the Supervised Machine Learning model in which the model finds the best fit linear line between the independent and dependent variable i.e it finds the linear relationship between the dependent and independent variable.
For example, say we have housing data with columns - “# of bedrooms”, “area sq ft”, “location”, “furnished”, “price”. Here we would be interested in knowing the price of the house given the rest of the features. The features can be continuous - “area sq ft”, discrete - “# of bedrooms” or even boolean - “furnished”.
We just need to make sure that the features are converted to numeric values. Once the preprocessing is done, we train the model to find a linear relationship between the rest of features and the price. This linear relationship is called Linear Regression. In other terms, “best fit”, something like…
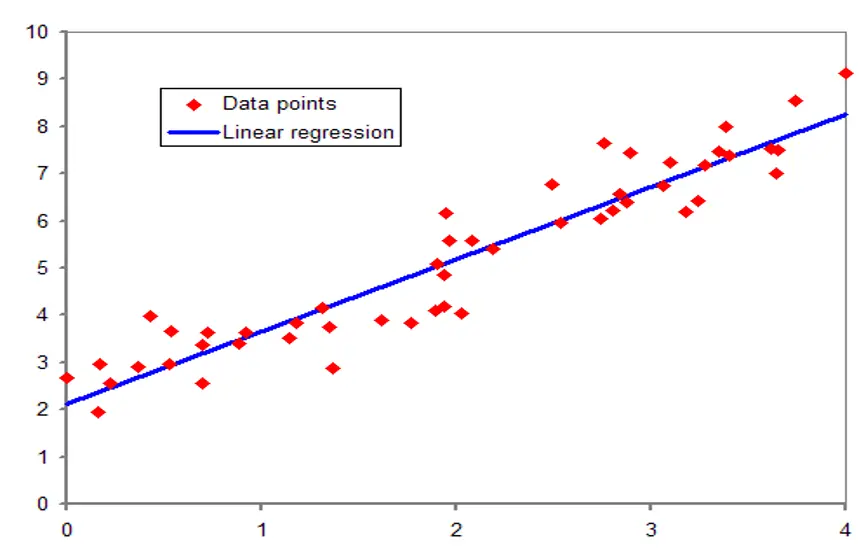
Figure 3. Linear Regression
2. How do we find the relation?
We find this relation using the equation:
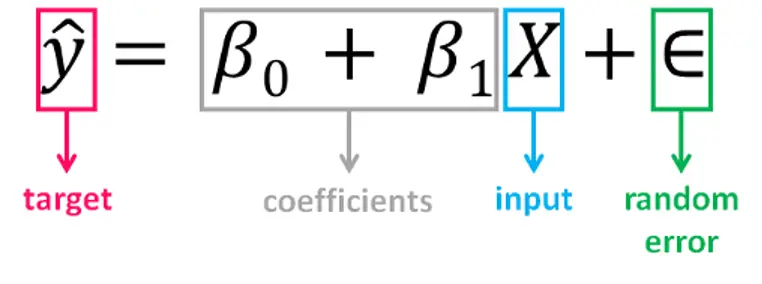
Figure 4. Linear Regression Equation
It’s a good idea to be familiar with a few terms like…
Independent Variable/Target variable:
Is the variable that we want to predict Eg. Price.
Dependent Variable/Input:
The variables used to predict the value of the output variable Eg. # of bedrooms, area sq ft, location, furnished.
β0/Intercept:
Point where the estimated regression line crosses the y-axis.
β1:
Slope of the regression line.
Error:
The random component of the linear relationship between the dependent and independent variables OR
the disturbance of the model, the part of y that X is unable to explain.
For the data we are using, the equation will look something similar to:
y = β0 + β1.#_of_bedrooms + β2.area_sq_ft + β3.location + β4.furnished + E
Finding the values of these constants (β1, β2, β3, β4) is what a regression model does by minimizing the error function and fitting the best line.
3. Cost Function
We can very well have multiple lines for different values of slopes and intercepts. But the main question that arises is which of those lines actually represents the best relationship between the dependent and target variables.
By achieving the best-fit regression line, the model aims to predict y value such that the error difference between predicted value and true value is minimum. So, it is very important to update the β1 values, to reach the best value that minimize the error between predicted y value (pred) and true y value (y). In other words we need to find the best values for β1, β2, β3, β4 for wich we use a Cost Function.
One of the Cost function(J) of Linear Regression is the Root Mean Squared Error (RMSE)
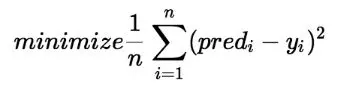
Figure 5. Cost Function
For more info on Cost Functions you can refer this link.
:
4. Assumptions of LR
There are some assumptions we need to consider while applying Linear Regression on any dataset:
1. Linearity:
Linearity means that a linear relationship already exists between Dependent Variables and Target Variable.
We just need to find that relaionship.
2. Independence:
Independence means that there is no relation between the data points i.e row #3 is independent of row #10.
All observations are independent of each other.
3. Homoscedasticity:
Homoscedasticity in a model means that the error is constant along the values of the dependent variable.
4. Normality:
For any fixed value of X, Y is normally distributed.
X = Dependent Variable
Y = Target Variable
References:
- https://www.kdnuggets.com/2020/10/guide-linear-regression-models.htm
- https://www.analyticsvidhya.com/blog/2021/03/data-science-101-introduction-to-cost-function/
- https://towardsdatascience.com/assumptions-of-linear-regression-fdb71ebeaa8b